TSM | Cronologia | Onomastico | Glossario | Thesaurus

De mensurabili musica

Trattato attribuito a Johannes de Garlandia, compilato dopo la metà del xiii sec., che sopravvive in tre codici collocabili fra la fine del xiii secolo e l'inizio del successivo:

—  B = Bruges, Stadsbibliotheek, ms. 528, ff. 54v-59v (fine xiii sec.)

 P = Paris, Bibliothèque nationale, Lat. 16663, ff. 66v-76v. (fine xiii sec. / ca 1300) [struttura dell'ultima sezione]

—  V = Roma, Bibl. Vaticana, Vat. lat. 5325, ff. 12v-30v (inizio xiv sec.)

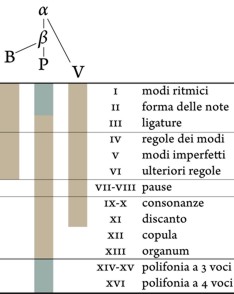
L'edizione critica di Reimer 1972 suppone V la copia più vicina all'archetipo, mentre B e P derivate entrambe da una stesura successiva. La suddivisione in 13 capitoli proposta da Reimer mostra come nessuna copia corrisponda all'originale: B trasmette solo la prima parte del trattato, V è privo degli ultimi due capitoli e P (la silloge di Hieronimus de Moravia) modifica i primi due e aggiunge i capp. xiv-xvi. P.

Edizione di V:

 Charles Edmond Henri de Coussemaker, Scriptorum de musica medii aevi novam seriem a Gerbertina alteram collegit, 4 voll., Parisiis: A. Durand, 1864-1876, i, pp. 175-182.
 Vers. digitale

Edizione di P:

 Charles Edmond Henri de Coussemaker, Scriptorum de musica medii aevi novam seriem a Gerbertina alteram collegit, 4 voll., Parisiis: A. Durand, 1864-1876, i, pp. 97-116.

Edizione critica:

  1. |  2. | Charles Edmond Henri de Coussemaker, Scriptorum de musica medii aevi novam seriem a Gerbertina alteram collegit, 4 voll., Parisiis: A. Durand, 1864-1876, i, pp. 175-182.
 Vers. digitale

Traduzioni inglesi (da Reimer 1972):

 Bob Richard Antley, The rhythm of medieval music · A study in the relationship of stress and quantity and a theory of reconstruction, with a translation of John of Garland's 'De mensurabili musica', PhD, Florida State University, 1977; Ann Arbor (Mich.): Umi, 1981.

 Johannes de Garlandia, Concerning measured music · De mensurabili musica, trad. ingl. di Stanley H. Birnbaum, Colorado Springs: Colorado College Music Press, 1978.

 

B/V   P [cap. I]  
Habito de ipsa plana musica, quae immensurabilis dicitur, nunc est praesens intentio de ipsa mensurabili, quae organum quantum ad nos appellatur, prout organum generaliter dicitur ad omnem mensurabilem musicam. Avendo discusso della musica monodica detta 'non misurata', ora è opportuno [parlare] di quella 'misurabile', ovvero di quanto chiamiamo organum, perché con organum intendiamo in generale tutta la musica mensurale. Habito, inquit Iohannes, de cognitione planae musicae et omnium specierum soni Avendo discusso, disse Giovanni, di cosa sia la musica monodica e delle varie forme del suono (degli intervalli),  
Unde organum et est species totius mensurabilis musicae et est genus diversimode tamen, prout dictum est superius.
Sciendum est ergo, quod ipsius organi generaliter accepti tres sunt species, scilicet discantus, copula et organum, de quibus dicendum est per ordinem.
Discantus est aliquorum diversorum cantuum sonantia secundum modum et secundum aequipollentis sui aequipollentiam.		 L'organum è 'forma' della musica misurata, o in altro senso 'genere', come s'è detto sopra.
Si deve quindi sapere che dell'organum in generale sono proprie tre forme: 'discanto', 'copula' e 'organo', di cui diremo in successione.
Discanto è il risuonare di più di un canto secondo il 'modo' e la relazione con il suono correlato. 		     
Sed quia in huiusmodi discantu consistit maneries sive modus, in primis videndum est, quid sit modus sive maneries, et de speciebus ipsius modi sive maneriei, et gratia huiusmodi maneriei ac specierum eius plura alia videbimus. Ma poiché in tal discanto si hanno 'specie' o 'modi', per prima cosa dobbiamo capire cosa sia 'modo' o 'specie' e quali forme abbia, e in ragione di tali 'specie' e relative forme comprenderemo altri aspetti. dicendum est de longitudine et brevitate eorundem, quae apud nos modus soni appellatur. dobbiamo dire della sua lunghezza e brevità, che noi chiamiamo 'modo del suono'.  
Maneries eius appellatur, quidquid mensuratione temporis, videlicet per longas vel per breves, concurrit. Si chiama 'specie' [del suono] ciò che concorre alla misura il tempo attraverso L e B. Unde modus est cognitio soni in acuitate et gravitate secundum longitudinem temporis et brevitatem. Il modo è la percezione dell'altezza e gravità del suono in funzione della lunghezza o brevità del tempo.  
    Et potest dupliciter sumi, aut communiter aut proprie. Modus communis est, qui versatur circa omnem longitudinem et brevitatem omnium sonorum. Modus proprius est, qui versatur circa sex modos antiquos. E [la parola] può essere usata in senso generale o proprio. Con 'modo' in generale ci si riferisce alla lunghezza e brevità di qualunque suono. In senso proprio si fa riferimento ai sei modi antichi.  
Sunt ergo sex species ipsius maneriei, quarum tres dicuntur mensurabiles, tres vero ultra mensurabiles, id est ultra rectam mensuram se habentes. Vi sono dunque 'specie' di sei forme, di cui tre si dicono 'a misura'; tre invece 'oltre misura', cioè che si estendono più della misura 'retta'.      
Iste vero dicuntur mensurabiles, scilicet prima, secunda et sexta. Iste vero ultra mensurabiles, scilicet tertia, quarta et quinta. Quelle dunque che si dicono 'a misura' sono la prima, la seconda e la sesta. Quelle invece 'extra misura' la terza, la quarta e la quinta. [cfr. 8]   [1]
Prima enim procedit ex una longa et altera brevi et altera longa, et sic usque in infinitum.
Secunda autem e converso, videlicet ex una brevi et altera longa et altera brevi.
Tertia ex una longa et duabus brevibus et altera longa.
Quarta ex duabus brevibus et altera longa et duabus brevibus.
Quinta ex omnibus longis.
Sexta ex omnibus brevibus. 		La prima [specie] inizia con una L, a cui segue una B, un'altra L, e così all'infinito.
La seconda sarà il contrario: ovvero una B, una L, un'altra B.
La terza una L e due B e una L.
La quarta due B, una L e due B.
La quinta tutte L.
La sesta tutte B. 		Quorum modorum primus constat longa brevi, longa brevi et caetera;
secundus brevi longa, brevi longa;
tertius longa duabus brevibus, longa duabus brevibus et caetera;
quartus duabus brevibus longa et caetera;
quintus omnibus longis;
sextus omnibus brevibus. 		Di cui il primo modo è formato da LB, LB etc.,
il secondo BL, BL,
il terzo LBB, LBB etc.,
il quarto BBL, etc.,
il quinto da tutte L,
il sesto da tutte B.		  
    Aliqui addunt modos alios, sed non est necessarium illos numerare, ut duae longae et brevis, quia per istos sex sufficientiam possumus habere. Qualcuno aggiunge altri modi che non è neccessario numerare, come LLB; e possiamo accontentarci di questi sei.  
[cfr. 4]   Omnium aliorum sonorum triplex est modus, unus in plenitudine vocis, alter est sub voce cassa, tertius sub voce amissa. Tutti gli altri suoni sono di tre tipi: a piena voce, a voce chiusa, a voce sfuggita. [2]
Gratia horum trium modorum, qui sunt in recto modo, videndum est, quid sit rectus modus et recta mensura.
Recta mensura appellatur, quidquid per rectam mensuram rectae longae vel rectae brevis profertur. 		In ragione dei tre modi che sono 'retti', vediamo cosa sia il 'modo retto' e la 'misura retta'.
Si chiama 'misura retta' ciò che risulta da una misura retta di L retta o B retta. 		     
Unde, ne in ambiguum procedamus, videndum est, quid appellatur recta longa vel recta brevis.
Ad quod dicendum, quod recta longa appellatur illa, quae continet duas rectas breves tantum. 		Per non precedere ambiguamente, dobbiamo vedere cosa significa L retta o B retta.
Si chiama L retta quella che contiene soltanto due B rette. 		[cfr. 6]   [3]
Recta vero brevis est, quae unum solum tempus continet. La B retta è quella che conta un solo tempo. Recta brevis est, quae unum tempus continet. La B retta è quella contiene un unico tempo.  
Propter hoc posset fieri quaestio, quid appellatur unum solum tempus. Ad quod dicendum, quod unum solum tempus, prout hic sumitur, est illud, in quo recta brevis habet fieri in tali tempore, quod fit indivisibile. A questo punto ci si può chiedere cosa sia un solo tempo. Un solo tempo, in questo caso, è quello in cui la B retta si completa in quello stesso tempo indivisibile      
Sed huiusmodi tempus habet fieri tripliciter: aliquando enim per rectam vocem, aliquando per vocem cassam, aliquando per vocem amissam. Ma qualunque tempo può essere in tre modi: con voce retta, con voce chiusa, con voce sfuggita. [cfr. 2]   [4]
Unde recta brevis habet fieri in primo tempore, videlicet per vocem rectam.
Sciendum est autem, quod huiusmodi duae tales breves, quae ita formantur, faciunt unam rectam longam.		 La B retta deve esser fatta nel primo tempo, ovvero con voce retta.
Si deve sapere quindi che due B siffatte producono una L retta.		 Unum tempus est, quod minimum in plenitudine vocis est.
Recta longa est duas rectas breves continens tantum. 		Un tempo è il minimo per la piena voce.
La L retta corrisponde a due B rette unite in una. 		 
Deinde accedendum est ad alias tres species, quae dicuntur ultra mensurabiles. Quindi trattiamo delle altre tre specie che si dicono 'oltre misura'.      
Unde ultra mensuram, prout hic sumitur, dicitur esse illud, quod ultra mensuram rectae longae vel rectae brevis profertur. Oltre misura, secondo quanto assunto, si dice essere ciò che è si estende più di una misura retta di L retta o B retta. Obliqua longa est, quae abundat super rectam longam. La L obliqua è quella che supera una L retta.  
    Duplex longa est, quae plures longas in se continet. Aliqua longa est, quae circumflectit se versus acuitatem vel gravitatem; et dicitur recta et obliqua. La DL è quella che contiene più L. Qualche L è tale che si piega all'acuto o al grave, e si dice 'retta' e 'obliqua'.  
 Ad hoc autem, quod possimus apprehendere, quid sit hoc dictum ultra mensuram, tres regulae sunt nobis necessariae.
Prima vero talis est: longa ante longam valet longam et brevem.
Secunda vero talis est: si multitudo brevium fuerit in aliquo loco, semper debemus facere, quod aequipolleant longis.
Tertia vero talis est: si multitudo brevium fuerit in aliquo loco, quanto brevis plus appropinquatur fini, tanto debet longior proferri. 		Dunque, per apprendere cosa sia 'oltre msura', tre regole sono necessarie.
La prima: L prima di L vale L + B.
La seconda: ovunque vi fosse un insieme di B, dobbiamo sempre farle corrispondere a una L.
La terza: ovunque vi fosse un insieme di B, quanto più la B si avvicina alla fine, tanto più deve essere allungata (resa L). 		[cfr. 7]   [5]
    Modorum alius perfectus, alius imperfectus. Dei modi [sia ha] il perfetto e l'imperfetto.  
Modus perfectus dicitur esse, quandocumque ita est, quod aliquis modus desinit per talem quantitatem vel per talem modum sicut per illam, qua incipit.
Dicitur modus perfectus, ut dicatur prima longa, altera brevis et altera longa, et sic de aliis modis sive maneriebus. 		Il modo perfetto si ha quando un modo finisce sulla quantità o modo con cui aveva cominciato.
Si dice modo perfetto quando ha la prima L, la seconda B e la successiva L e così per gli altri modi o maniere. 		Perfectus modus dicitur, qui finit per talem quantitatem, per qualem incipit, ut longa brevis longa. Il modo perfetto è quello che comincia con la quantità con cui inizia, come L B L.  
Omnis modus dicitur imperfectus, quandocumque ita est, quod aliquis modus desinit per aliam quantitatem quam per illam, qua incipit, ut cum dicatur prima longa, altera brevis, altera longa et altera brevis. Ogni modo imperfetto finisce per quantità diversa da quella con cui comincia, come quando si abbia la prima L la seconda B, poi L e poi B. Imperfectus est, qui terminatur per aliam quam per illam, in qua incipit. Sic apparet, quod sunt duodecim modi cum perfectis et imperfectis sine aliis. Quello imperfetto comincia con quantità diversa da quella con cui ha iniziato. Ecco perché ci sono solo 12 modi fra perfetti e imperfetti. [cioè 6 perfetti e 6 imperfetti]  
[cfr. 3]   Modus rectus est, qui procedit per rectas longas et rectas breves. Il modo retto è quando si usano L rette e B rette. [6]
    Obliquus est, qui procedit per aliquas longas et aliquas breves. L'obliquo si ha con qualunque tipo di L e B.  
[cfr. 5]   Regula cognitionis temporum:
[Prima:] longa ante longam valet tria tempora.
Secunda regula est: duae rectae breves valent unam rectam longam.
Tertia regula est: multitudo brevium simul quanto magis appropinquatur fini, tanto debet longior proferri. 		Regola della gestione del tempo:
[Prima:] L davanti a L vale tre tempi.
Seconda: due B rette valgono una L retta.
Terza: con molte brevi insieme man mano che ci si avvicina alla fine, tanto più deve essere allungata (resa L). 		[7]
[cfr. 1]   Unde sequitur, quod primus, secundus, sextus dicuntur modi recti, tertius, quartus, quintus dicuntur obliqui. Dunque se primo, secondo e sesto modo sono retti, terzo, quarto e sesto sono obliqui. [8]
    Sed aliqui volunt, quod quintus noster modus sit primus omnium. Et bona est ratio, quia per istum modum praecedit omnes nostros modos. Sed quoad tempora cognoscenda prius est modus rectus quam obliquus, et sic non valet, quod dicitur, quod quintus est primus. C'è chi vuole che il nostro quinto modo sia il primo di tutti. E vi son buone ragioni perché questo modo preceda tutti gli altri, ma per comprendere il tempo il modo retto deve precedere l'obliquo e si vanificherebbe quanto detto se il quinto fosse primo.  
    Ordo modorum est numerus punctorum ante pausationem. Iste ordo dividitur in primum, secundum et tertium et caetera. Ordo autem procedit ab uno principio, principium a radice. Radix est quilibet cantus primo datus.
Exemplum primum primae radicis:


Latus

Et notandum, quod principium cuiuslibet modi caret omni pausatione.		 L'ordo modale è l'insieme delle note [«punctorum»] prima della pausa. Gli ordines si contano come primo, secondo, terzo etc. L'ordo procede da un esordio unitario, l'esordio da una 'radice'. La 'radice' è l'inizio di un qualunque canto.
Primo esempio di prima radice:
— 2cc Lcc Lcc 2cc Lcc 3 2 2 2 2 2 2 2 2 2
Si noti che all'inizio di qualunque modo manca sempre la pausa.		  
Exemplum primae maneriei de perfecto modo:
— 3 2 2 B-L 2 2 2 || 3 | L L | 3 | 3 | 3 2-L
Exemplum primae maneriei de imperfecto modo:
— L 2 2 2 2-B
Exemplum secundae de perfecto modo:
— 3 | 2-B | 3 | 3 | L L | 3 | 3 | 2-B ||
Exemplum secundae de imperfecto modo:
— L 3 3 3 2p | BL 2 2 2 2
Exemplum tertiae de perfecto modo:
— L 3 3 2-L
Exemplum tertiae de imperfecto modo:
— L 3 3 2
Exemplum quartae de perfecto modo:
— 3 B-2 3 2
Exemplum quartae de imperfecto modo:
— 3 B-2 3 4
Exemplum quintae de perfecto modo:
— L L L L L | L L L L L L L L L L
Exemplum quintae de imperfecto modo:
— L L L L | L L L L | L L L L |
Exemplum sextae de perfecto modo:
— L 3 2-B | 2-2-B-2 | B-3
Exemplum sextae de imperfecto modo:
— 2 2 2-2 B-2-B-B		   Primus ordo primi modi perfecti*    
  * Il codice tronca la frase che Hieronimus derivava dall'Anonimo iv: «Primus ordo primi perfecti est trio punctorum cum una brevi pausatione et trio punctorum cum pausatione brevi et trio punctorum cum pausatione brevi» = ligatura a 3 [LBL] + pausa di B – Poi, forse accorgendosi di descrivere informazioni già ripetutamente affrontate, passa direttamente a considerazioni sulla combinazione dei modi.    
    Modus obliquus habet plures considerationes, ut patet in tertio, quia tertius constat ex longa et duabus brevibus, et duae breves aequipollent longae, et longa ante longam valet longam et brevem, et sic valet tria tempora; quare longa ante duas breves valet tria tempora, et sic valet longam et brevem vel brevem et longam.
Item duae breves aequipollent longae, ergo si ponantur ante longam, valent tria tempora, ergo valent longam et brevem vel e converso. 		Il modo obliquo merita alcune osservazioni, come appare nel terzo [modo], poiché il terzo consta di una L e due B, e le due B corrispondono alla L, e la L prima di una L vale L + B, cioè 3 tempi; similmente L davanti a due B vale 3 tempi e altrettanto vale L + B o B + L.
Inoltre due B equivalgono a una L, ma se si pongono davanti a una L valgono 3 tempi, cioè L + B o il contrario.		  
    Unde regula: si sint plures breves in modis obliquis, quae magis appropinquatur fini, longior debet proferri, ergo illae duae valent brevem et longam, et non longam et brevem.
Quare tertius modus et quartus potius reducuntur ad secundum quam ad primum. 		La regola: essendovi più B nei modi obliqui, poiché avvicinandosi alla fine devono allungarsi, allora due B valgono B + L e non L + B.
Perciò il terzo e quarto modo si possono ricondurre al secondo piuttosto che al primo. 		 
    Sed quintus indifferenter ad primum et secundum potest reduci. Unde quintus modus constat ex omnibus longis.
Et sic quaelibet longa est ante aliam longam, quare quaelibet valet tria tempora confuse et non distincte, et sic valet longam et brevem vel e converso.
Et sic potest reduci ad primum et secundum confuse, et mediante secundo potest reduci ad tertium et ad quartum.
Quamvis omnes modi et ad primum et ad secundum possunt reduci, sed in isto modo aliter respicimus pausationem quam in aliis modis, cum in aliis modis quanta est paenultima, tanta est pausatio.
Et hic ex toto ista regula non observatur, sed in parte, quia est pausatio longa et aliquotiens brevis, sive fuerit perfectus sive imperfectus: sed si fuerit longa, erit propria sua pausatio, brevis accommoda, ut in sequentibus patebit. 		Invece il quinto modo può essere unito indifferentemente al primo o al secondo, perché il quinto consta di sole L.
E perciò qualunque L davanti ad altra L vale sempre tre tempi (uniti e non distinti), similmente si comportano L+B o viceversa.
E così può essere unito indifferentemente al primo o al secondo modo, e attraverso il secondo può essere unito al terzo e al quarto.
Benché qualunque modo possa essere unito sia al primo che al secondo, tuttavia in questo [quinto] modo determiniamo diversamente le pause che negli altri, perché negli altri modi la pausa vale quanto la penultima nota.
E in questo caso la regola è osservata solo in parte, poiché a volte la pausa è lunga a volte breve: nel caso che sia lunga la pausa sarà propria, se breve sarà adattata come apparirà più avanti. 		 
    Sextus modus potest reduci ad primum vel secundum. Sed quando reducitur ad primum, terminatur in longam et habet pausationem unius temporis.Quando autem reducitur ad secundum, tunc finitur per brevem et habet pausationem duorum temporum.
Sed ad proprium modum totaliter non fit, sed circulariter soni ultimi et pausationes breves semper et in ordinibus sive perfectis sive imperfectis secundum magis et minus ad modum tertii perfecti et imperfecti erunt. 		Il sesto modo si può unire al primo o al secondo, ma quando si unisce al primo termina con L e ha la pausa di un tempo; quando invece si unisce al secondo allora termina con B e ha pausa di due tempi.
Ma se non seguisse interamente il proprio modo, ma occasionalmente [«circulariter»], allora gli ultimi suoni e pause B seguiranno sempre l'ordo, sia perfetto sia imperfetto, più o meno come con il terzo modo perfetto o imperfetto.		  
  [cap. II]      
Sequitur de repraesentatione figurarum sive notularum, videlicet quomodo per huiusmodi figuras denotetur longitudo vel brevitas. Segue la forma delle figure o note, ovvero in che modo per qualunque figura sia distinta per lunghezza o brevità. Habito de modis existunt et de eorum partibus sequitur de figuris et eorum significationibus.    
Unde figura est repraesentatio soni secundum suum modum. La 'figura' è rappresentazione del suono secondo il suo modo. Figura, ut hic accipitur, est signum denotans sonum vel sonos secundum suum tempus longitudinis atque brevitatis.    
Et sciendum, quod huiusmodi figurae aliquando ponuntur sine littera, aliquando cum littera; sine littera ut in caudis vel conductis, cum littera ut in motellis.
Inter figuras, quae sunt sine littera et cum littera, talis datur differentia, quoniam ille, quae sunt sine littera, debent, prout possunt, amplius ad invicem ligari.
Sed huiusmodi proprietas aliquando amittitur propter litteram huiusmodi figuris associatam.
Sed huiusmodi figurarum tam litterae societarum quam non societarum dantur divisiones sequentes ac etiam regulae.		 E si sappia che di qualunque modo [siano] a volte si dispongono in forma 'melismatica', a volte 'sillabica': melismatica come nelle 'code' o conductus, sillabica come nei mottetti.
Fra le figure melismatiche o sillabiche questa è la differenza: poiché quelle che sono melismatiche dovono essere legate fra loro per quanto possibile.
Tale proprietà a volte si sospende in ragione della sillabazione associata a tal figura.
Sia delle figura unite che separate si danno le 'figure' seguenti e anche le regole.		      
Prima divisio est haec: figurarum quaedam ligantur ad invicem, quaedam non. La prima caratteristica è questa: fra le figure alcune legano [note] fra loro, altre no. Figurarum quaedam simplex, quaedam composita vel ligata, quod idem est.    
Figura ligata est, ubicumque fit multitudo punctorum simul iunctorum per suos tractus. Figura non ligata est, ubicumque non fit multitudo punctorum et caetera, vel etiam simplex. La ligatura [«figura legata»] è sempre un insieme di punti congiunti fra loro con proprio tratto. La 'figura' non legata è quando non vi sia un insieme di punti etc., ovvero [ogni punto/nota] sia semplice.    
Figurarum simplicium quaedam dicuntur longae, quaedam breves.
Longarum triplex est modus, quia quaedam dicitur recta longa, quaedam duplex longa, quaedam plica longa.
Unde sequitur regula: omnis figura simplex portans tractum magis a parte dextra quam a sinistra semper significat longitudinem.
Recta longa est illa, quando longitudo non transit latitudinem.
Duplex longa est illa, quando latitudo transit longitudinem.
Plica longa dicitur illa, quae habet duplicem tractum, scilicet a parte dextra longiorem quam a sinistra, et est duplex, ascendendo et descendendo.		 Delle figure semplici alcune sono lunghe altre brevi.
Delle longae triplice è il modo: 'longa retta', duplex longa, e plica.
Da cui segue la regola: il tratto lungo a destra o a sinistra delle figure singole determina sempre la durata.
La L retta si ha quando la larghezza non supera l'altezza.
La duplex L si ha quando la larghezza supera l'altezza.
La lunga piegata è quella che ha duplice tratto, ovvero a destra più lungo che a sinistra, e doppio, salendo e discendendo.		 Simplicium quaedam dicitur longa, quaedam brevis.
Longarum, quae dicuntur puncta longa, triplex est modus, scilicet recta longa et superabundans et plica longa.
Recta longa est, cuius latitudo non transit longitudinem cum tractu descendente a parte dextra, ut hic: L L L
Superabundans sive duplex longa, quod idem est, cuius latitudo transit longitudinem cum tractu praedicto, ut hic declaratur: MX MX MX
Plica duplex est, ascendens et descendens. Descendens cum duplici tractu fit, ascendens cum uno tantum vel duplici, sed semper est longior tractus a parte dextra, ut hic: [esempio] 		   
Similiter brevium triplex est modus. Quaedam dicitur recta brevis, quaedam semibrevis, quaedam plica brevis. Omnis figura brevis sumitur sine tractu praeter plicam, quae accipitur cum duplici tractu vel uno propter divisionem soni.
Similiter etiam duplex est plica, quia quaedam dicitur ascendendo, quaedam descendendo, ut superius dicebatur.
Semibrevis est, quae formatur ad modum rectae brevis, sed quatuor anguli transpositi ad differentiam rectae brevis.		 Similmente delle brevi ci sono tre forme. Una si dice brevis retta, una semibrevis, una brevis plicata. Tutte le figure brevi sono impiegate senza tratto, tranne quelle plicate che accolgono uno o due tratti.
Similmente duplice è anche la [B] plicata, poiché una si dice ascendente, una discendente, come sopra accennato.
S è quella che si forma al modo della breve ma con i quattro angoli ruotati differentemente dalla B retta.		 Brevium triplex est modus, scilicet recta brevis recte posita, et est, cuius latitudo non transit longitudinem et sine tractu, ut hic patet: B B B B
Et est semibrevis oblique posita, ut hic apparet: S,S,S,S,S
Est et alia plica brevis et fit, quando longior tractus fit a parte sinistra, ut hic: [esempio]		    
Figurarum simul ligatarum quaedam dicitur ascendendo, quaedam descendendo. Figura descendendo dicitur esse illa, quando secundus punctus ligaturae inferior est primo. Ascendendo dicitur esse, quando secundus punctus altior est primo.
Figurarum ascendendo vel descendendo duae sunt species, quia quaedam dicitur cum proprietate a parte principii, quaedam a parte finis.		 Delle figure legate insieme una si dice ascendente, una discendente. La figura discendente si dice essere quella che ha il secondo punto della legatura inferiore al primo. Ascendente quando il secondo punto è più alto del primo.
Delle figure, ascendenti o discendenti, due sono le forme, poiché una si dice 'propria' [«cum proprietate»] secondo 'inizio' o 'fine'.		 Figura composita vel ligata est, quando plura puncta in unum coniunguntur a puncto ad puncta ascendentes vel descendentes [esempio]
Figurarum quaedam dicuntur ascendendo, quaedam descendendo, et hoc a parte principii vel finis.
Item quaedam dicuntur perfectae, item quaedam cum proprietate, quaedam sine. Descendens dicitur figura, quando secundus punctus inferior est primo, ascendens e converso.		    
A parte principii quatuor sunt species, quia quaedam dicitur cum proprietate, id est cum proprietate propria, quaedam sine proprietate, quaedam per oppositum cum proprietate, quaedam sine opposito cum proprietate. Quattro sono le forme d'inizio: una si dice 'propria', una 'impropria', una 'con proprietà opposta', una 'senza proprietà opposta'.      
Unde regula: omnis figurae descendendo proprietas est, ut primus punctus habeat tractum a latere sinistro. Ascendendo proprietas est, ut nullum habeat tractum.
Ascendendo sine proprietate, ut habeat tractum, descendendo, ut non habeat.		 Onde la regola: sono 'proprie' tutte le figure discendenti in cui la prima nota [«punctus»] abbia il tratto sul lato sinistro. Ascendendo sono 'proprie' quando senza tratto.
L'ascendente 'proprio' ha il tratto, il discendente non ce l'ha.		 Cum proprietate descendente dicimus, quando primus punctus habet tractum descendentem a latere sinistro. Si tractus fuerit ascendens, cum proprietate opposita dicetur, ut hic: [esempio]
In figura ascendente proprietas sua est, quando primus punctus non habet tractum, ut hic patet: [esempio]
Sed sine proprietate dicitur, si habet tractum, ut hic: [esempio]
Et sic intelligimus de figura descendente ad suum contrarium, ut hic: [esempio]		    
Ascendendo vel descendendo dicitur per oppositum cum proprietate, ut primus punctus habeat tractum ascendendo a latere sinistro, sine opposito, ut non habeat tractum. Ascendedo o discendendo si dice 'con opposta proprietà' quando la prima nota ha il tratto ascendente a sinistra, senza non ce l'ha.      
A parte finis etiam quatuor sunt species, quia quaedam dicitur cum plica, quaedam sine plica, quaedam perfecta circa finem, quaedam imperfecta circa finem.
Cum plica dicitur esse illa, quando ultimus punctus portat tractum a parte dextra, et hoc est dupliciter, aut ascendendo aut descendendo. Sine plica dicitur, quae non habet tractum		 Anche alla fine vi sono quattro forme [di 'proprietà'], poiché una si dice plicata, una non plicata, una perfetta alla fine, una imperfetta alla fine.
Plicata è quando l'ultima nota porta il tratto a destra in due modi: ascendente o discendente. Non plicata è quando non ha il tratto.		      
Perfecta circa finem dicitur dupliciter, aut ascendendo aut descendendo. Ascendendo dicitur esse, quando ultimus punctus ligaturae altior est paenultimo. Descendendo est, quando ultimus punctus inferior est paenultimo.
Perfecta ascendendo est illa, quando ultimus punctus stat perpendiculariter supra paenultimam. Imperfecta est, quando stat obliquo modo.
Perfecta descendendo est, quando tractus a paenultimo punctu usque ad ultimum stat perpendiculariter. Imperfecta dicitur, quando tractus a paenultimo usque ad ultimum stat obliquo modo. 		Perfetta alla fine si dice in due modi: ascendente o discendente. Ascendendo si dice quando l'ultimo punto della legatura è più alto del penultimo. Discendendo è quando l'ultimo punto è inferiore al penultimo.
Perfetta ascendente è quella quando l'ultimo punto è perpendicolare sopra il penultimo. Imperfetta quando è in modo obliquo.
Perfetta discendendo è quando il tratto dal penultimo punto all'ultimo è perpendicolare. Imperfetta quando il tratto dal penultimo all'ultimo è obliquo.		 Figura perfecta in fine dicitur, quando tractus a paenultima ad ultimam fuerit descendens perpendiculariter, et hoc in figura descendente in fine. Et hoc est, quando ultima fuerit inferior paenultima, ut hic: [esempio]
Sed in figura ascendente in fine est perfectio, cuius ultimus punctus recte iacet supra paenultimum: [esempio]
Imperfecta vero dicitur, sive fuerit ascendens sive descendens, si ultimus punctus fuerit obliquus ad paenultimam, ut hic patet: [esempio]		    

 

B/P/V [cap. III]
Sequitur de regulis figurarum ad invicem ligatarum cum proprietate vel sine proprietate et caetera.
Omnis figura ligata cum proprietate posita et perfecta paenultima dicitur esse brevis et ultima longa.
Si sint ibi praecedentes vel praecedens, omnes ponuntur pro longa.
Omnis figura sine proprietate et perfecta posita valet per oppositum cum proprietate.
Regula est, quod numquam ponuntur duae breves vel tres vel quatuor et caetera pro brevi, ubi possunt poni pro longa.
Omnis ligatura per oppositum cum proprietate et perfecta ultima est longa et omnes praecedentes ponuntur pro brevi, si sint ibi plures sive pauciores.
Omnis figura cum plica et cum proprietate et perfecta ultima cum plica valet longam, quia plica nihil aliud est quam signum dividens sonum in sono diverso. Omnis figura cum plica et sine proprietate et perfecta ultima cum plica dicitur esse brevis, et ita sunt duae breves, id est semibreves.
Omnis figura cum plica et cum opposita proprietate sumitur ut cum proprietate vel non et perfecta.		 Seguono le regole delle figure legate a vicenda con proprietà o senza proprietà etc.
In ogni legatura che si mostra 'propria' e 'perfetta', la penultima [nota] si dice essere B e l'ultima L.
Se vi sono una o più [note] precedenti, tutte occupano lo spazio di una L.
Ogni figura che si mostra 'impropria' e 'perfetta', vale l'opposto [di quella] 'propria'.
La regola è che mai si danno due B o tre o quattro etc. al posto di una B dove possono stare al posto di una L.
In ogni legatura con proprietà opposta e perfezione, l'ultima [nota] è L e tutte le precedenti occupano lo spazio di una B, che siano poche o tante.
In tutte le figure plicate, proprie e perfette, l'ultima plicata è L, poiché la plica non è altro che un segno che divide il suono in suono diverso.
Ogni figura plicata, senza proprietà e perfezione, l'ultima plicata si dice essere B, e perciò sono due B, cioè semibrevi.
Ogni figura con plica e con proprietà opposta si intende come con proprietà o senza e perfezione
Ogni figura imperfetta s'intende in tre modi: 'propria', plicata o meno; 'impropria', plicata o meno; 'con proprietà opposta', plicata o meno, come [era con la figura] perfetta.
La regola: ogni figura imperfetta, se 'propria' giunge fino alla prima L successiva, se 'impropria' giunge fino alla prima B successiva.
E tutto ciò si capisce nei conductus o mottetti quando si adotta [la forma] melismatica o sillabica, se sono scritti in modo 'proprio'. Se sono scritti in modo 'improprio', tutte le figure diventano imperfette, e ciò si capisce nel discanto, e ovunque si abbia il giusto modo. 		Omnis figura imperfecta sumitur tripliciter: aut cum proprietate et cum plica vel sine plica, aut sine proprietate et cum plica vel sine plica, / [P 68rb in marg.] aut per oppositum cum proprietate ‹et› cum plica vel sine plica ut perfecta. Regula est: omnis imperfecta figura, si sit cum proprietate, extenditur usque ad primam longam sequentem, si sit sine proprietate, extenditur usque ad primam brevem sequentem.
Et totum hoc intelligitur in conductis vel motellis, quando sumuntur sine littera vel cum littera, si proprio modo figurantur. Si improprio modo figurantur, fere omnes figurae accipiuntur imperfectae, et hoc intelligitur in discantu et ubicumque rectus modus accipitur.
B/P/V [cap. IV]
Sequitur de probatione modorum per figuras.
Unde prima regula primi modi dicitur esse tres ligatae ad invicem in principio et in posterum cum duabus et duabus ligatis et caetera, et hoc totum cum proprietate et perfectione, ut hic: [esempio]
Alia regula de eodem: tres ligatae cum brevi pausatione et caetera in infinitum, et hoc potest intelligi, ut sumitur hic: [esempio]
Secundi modi prima regula sumitur ita: duae et duae cum proprietate et caetera et tres in fine sine proprietate et ‹perfectae›, ut sumitur hic: [esempio]
Alia regula de eodem: tres sine proprietate cum longa pausatione et sic in infinitum, ut sumitur hic: [esempio]
Tertius modus dicitur ita per figuram: prima longa et tres ligatae et tres et tres, et hoc cum proprietate, ut hic: [esempio]
Quartus modus dicitur ita: tres et tres et tres ligatae cum proprietate et duae imperfectae in fine cum longa pausatione, ut hic: [esempio]
Quintus modus sumitur hoc modo: omnes longae, ut hic: [esempio]
Alia regula de eodem: tres et tres ligatae cum proprietate et perfectae cum longa pausatione et caetera, et hoc fit causa brevitatis et non proprie dicitur ita, sed usus est, quod ita in tenoribus motellorum accipiatur, ut hic: [esempio]
Sextus sumitur hoc modo: quatuor ligatae cum proprietate et plica et postea duae ligatae ‹cum plica› et duae cum plica et caetera, ut hic: [esempio]
Alia regula de eodem, sed non probatur per istam artem, sed bene probatur per exemplum, quod invenitur in alleluia Posui adiutorium in triplo, scilicet quatuor ligatae cum proprietate et postea tres et tres et tres cum proprietate et caetera, et hoc est exemplum, quod sumitur in supradicto Alleluia: 		Segue la verifica delle forme secondo la figura.
Onde la prima regola del primo modo dice esserci tre [note] legate fra loro al principio e poi due a due etc. e questo sempre con proprietà e perfezione, così: [esempio]
Altra regola dello stosso: tre legature con pausa di B etc. all'infinito, e questo si può capire, come si mostra qui: [esempio]
Per il secondo modo la prima regola può essere mostrata così: due e due 'proprie' etc. e tre in fine 'improprie e 'perfette', come si mostra qui: [esempio]
Altra regola dello stesso: tre 'improprie' con pausa di L e così all'infinito, come si mostra: [esempio]
Il terzo modo secondo la figura appare così: prima L e tre legate e tre e tre, e questo con proprietà, così: [esempio]
Il quarto: tre e tre e tre legature 'proprie' e due imperfette in fine con pausa di L, così: [esempio]
Il quinto: tutte lunghe: [esempio]
Altra regola dello stesso: tre e tre legate, proprie e perfette, con pausa di L etc. e questo si adotta per comodità ed è detto tale impropriamente, ma è adottato nei tenores dei mottetti, così: [esempio]
Il sesto: quattro [note] legate, proprie e plicate, e poi due legate [e plicate] e due plicate etc., così : [esempio]
Altra regola dello stesso, che tuttavia non si approva come modello, ma solo come caso: quanto propone l'alleluia Posui adiutorium a tre voci, ovvero: ligatura a quattro propria, e dopo tre, tre, tre poprie etc., e questo è l'esempio del suddetto alleluia:
  F, f. 36r   Mo, f. 16v
B/P/V [cap. V]
Sequitur de modis imperfectis, quomodo et qualiter figurantur.
Unde primus modus imperfectus figuratur hoc modo: tres cum proprietate et postea cum duabus et duabus et caetera cum proprietate et in fine tres sine proprietate, ut hic: [esempio]
Alia regula de eodem: duae ligatae et duae sine proprietate et cum proprietate et cum pausatione longa et brevi, ut hic: [esempio]
Secundus modus imperfectus sumitur hoc modo: duae ligatae et duae cum proprietate, ut in hoc exemplo: [esempio]
Alia regula de eodem: duae cum proprietate ‹cum brevi› pausatione et etiam duae sine proprietate cum longa pausatione, ut hic: [esempio]
Tertius modus imperfectus sumitur hoc modo: scilicet una longa cum tribus et tribus et tribus ligatis cum proprietate et in fine duae cum proprietate et imperfectae, ut hic: [esempio]
Quartus modus imperfectus sumitur hoc modo: scilicet tres et tres ligatae cum proprietate, ut hic: [esempio]
Quintus modus imperfectus sumitur hoc modo: omnes longae in pari numero, ut hic: [esempio]
Sextus modus imperfectus sumitur hoc modo: quatuor ligatae cum plica primo, postea cum duabus et duabus cum proprietate et cum plica, si reducatur ad primum modum, ut hic: [esempio]
Si modus iste accipitur per reductionem secundi, talis est regula: duae ligatae et duae, duae et caetera cum proprietate et perfectae et cum plica, omnes breves dicuntur, ut sumitur in hoc exemplo: [esempio]
Et hoc est propositum omnium modorum perfectorum et imperfectorum. 		 
B/P/V [cap. VI]
Sed sciendum, quod numquam debet poni aliqua figura sine proprietate, ubi potest poni cum proprietate. Alia regula, quod numquam ponatur simplex vel non ligata, ubi potest poni ligata vel composita. Omnis ordinatio ligatarum debet fieri per eundem ordinem compositarum, id est per eandem ligaturam. Omnis figura simplex sumitur secundum suum nomen, sive fuerit cum littera sive non. Item omnes voces, quae accipiuntur in eodem sono, non possunt ligari vel facere figuram compositam, quia omnis figura composita vel ligata dicitur ascendendo vel descendendo. Et quaecumque sunt in eodem sono, non sunt ascendendo vel descendendo, ergo ex his non fit ligatura, id est figura ligata. Item omnis figura non ligata debet reduci ad figuram compositam per aequipollentiam. Item omnis figura ligata ultra tres suo proprio modo reducitur ad tres per aequipollentiam. Item omnis figura simplex, id est non composita, et duae ligatae sequentes reducuntur ad tres ligatas per aequipollentiam, et hoc est secundum propriam proprietatem, quia reducuntur ad aliquem modum proprium. Item, ubicumque invenitur multitudo brevium, semper participant cum praecedente, quia praecedens cum eis non reputatur, nisi pro uno tali sicut et praecedens.